【数的処理】組み合わせの問題【No.77】

次の図において、AからBまで最短距離を通って行く方法は何通りあるでしょうか。
①52 ②57 ③63 ④66 ⑤72
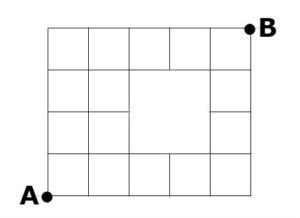
【解答】
図を分かりやすくするように書くと
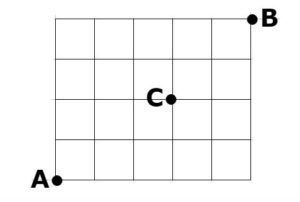
このように通ってはいけない箇所をCとする
AからBまでは9マスである
そのうち縦が4マス、横が5マスなので、AからBへ最短距離で行く方法は
$$\small\frac{9!}{5!・4!}=\frac{9・8・7・6・5・4・3・2・1}{5・4・3・2・1・4・3・2・1}$$
$$=126$$
Cの箇所は通っていけないので、全体の126通りからCを通るルートを引かなければならない
まずAからCのルートは
$$\frac{5!}{3!・2!}=10$$
次にCからBのルートは
$$\frac{4!}{2!・2!}=6$$
よって、A→C→Bと通るルートは
10×6=60通り
なので、Cを通らずにAからBへ最短距離で向かうルートは
126-60=66通り
答え・・・④
最短距離の問題は
$$\frac{全移動マス!}{縦マス!×横マス!}$$
で解きますので、覚えておきましょう。
選んで損しない、数的処理のおすすめ問題集
- 畑中敦子の数的推理ザ・ベストプラス【第2版】
▶︎問題の難易度はバランスよく掲載されています。万人向けのベストセラー。
- 公務員試験 新スーパー過去問ゼミ5 数的推理
▶︎問題の難易度は高め。数的処理の腕試しがしたい人向け。
- 数的推理がみるみるわかる! 解法の玉手箱 改訂第2版
▶︎数的処理が苦手な人向け。問題の難易度は低め。
【数的処理】組み合わせの問題【No.78】
AからEの5つのクラスから8人の生徒を委員に選ぶ。各クラスから少なくとも1人は選ばなければいけないとすると、8人のクラスの組み合わせは何通りあるでしょうか。
①15 ②25 ③35 ④45 ⑤55
【解答】
8人のうち各クラスから必ず1人ずつは選ばれるというので、残り3人の所属するクラスを考える。
3人全て同じクラスの場合・・・5通り
3人のうち2人が同じクラスの場合・・・20通り
3人の所属するクラスがバラバラの場合、5クラスの中から3クラスを選ぶということなので
$${}_5 \mathrm{C} _3=\frac{5・4・3}{3・2・1}=10$$
よって、5+20+10=35
答え・・・③
私が自信を持ってオススメする数的処理の問題集
社会人から公務員へ転職する方へ
公務員試験の論文の最強のテンプレート
































