【数的処理】公務員試験に向けて問題をやってみよう【002】

【数的処理】n進数の演算【No.5】

二進法で表された数1011と三進法で表された数2022の積を五進法で表しなさい。

 

【解答】

1011を10進法に置き換えると、

$$1011⇒(1×2^3)＋(0×2^2)＋(1×2^1)＋1=11$$

2022を10進法に置き換えると、

$$2022⇒(2×3^3)＋(0×3^2)＋(2×3^1)＋2=62$$

10進法で表したこれら2つの積は、

$$11×62=682$$

 

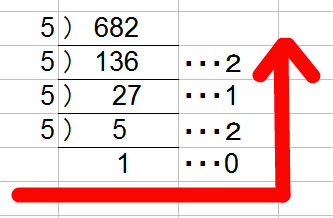
682を五進法で表せというのだから、ずっと5で割っていき、余りを右側に書いていく。

最後に5÷5=1のときの余り=0を書き忘れないように注意すること！

余りを矢印の方向の順に書いていったものが682を五進法で表したものなので、

$$682（5進法）=10212$$

答え・・・10212

 

ちなみに、数的処理がどうにもこうにも苦手・・・といったように、数的処理に対して苦手意識がある人はぜひ下記の記事を読んでみてください。

 

【練習問題1】

二進法で表された1011と二進法で表された1101の和を二進法で表しなさい。

 

【解答】

1011を10進法に置き換えると、

$$\small1011⇒(1×2^3)＋(0×2^2)＋(1×2^1)＋1=11$$

1101を10進法に置き換えると、

$$\small1101⇒(1×2^3)＋(1×3^2)＋(0×2^0)＋1=13$$

10進法で表したこれら2つの和は、

$$11＋13=24$$

 

 

24を二進法で表せというのだから

ずっと2で割っていき、余りを右側に書いていく。

$$24（2進法）=11000$$

答え・・・11000

 

選んで損しない、数的処理のおすすめ問題集

【数的処理】整数の比の問題【No.6】

2つの正の整数の比が9:4で、その積は324になるという。この2数の差はいくらでしょうか？

 

【解答】

$$2つの正の数を9xと4xとおきます。$$

$$その積が324なので、9x・4x=324$$

$$36x^2=324$$

$$x=\pm3$$

よって2つの正の数は27と12

この2つの数の差を求めなさいという事なので、

$$27-12=15$$

$$　= \color{red}{15・・・ （答え）}$$

 

▶︎合格する人はみんなやってる！公務員試験の勉強の予定立ては、これを使えば完璧！

【数的処理】年齢の問題【No.7】

現在、父の年齢は母の年齢より6歳多くて34歳、3人の子供の年齢の和は11である。父母の年齢の和が3人の子供の年齢の2倍になるのは何年後でしょうか。

 

【解答】

父の年齢・・・34歳
母の年齢・・・28歳
子供3人の年齢の和・・・11歳

$$父と母の年齢の和が3人の子供の年齢の$$
$$2倍になるのをx年後とすると、$$

$$(34＋28＋2x)=2(11＋3x)$$

$$2x＋62=22＋6x$$

$$4x=40$$

$$x=10$$

答え・・・10年後